El movimiento Bidimencional Parabolico
Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.
Puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.
Tipos de movimiento parabólico
- El movimiento de media parábola o semiparabólico (lanzamiento horizontal)
- se puede considerar como la composición de un avance horizontal rectilíneo uniforme y la caída libre.
- El movimiento parabólico completo
- se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUA) por la acción de la gravedad.
En condiciones ideales de resistencia al avance nulo y campo gravitatorio uniforme, lo anterior implica que:
- Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.
- La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.
- Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente completo que alcance la misma altura tarda lo mismo en caer.
Ecuaciones del movimiento parabólico
Hay dos ecuaciones que rigen el movimiento parabólico:
donde:
 es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial. es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal. es la aceleración de la gravedad.
es la aceleración de la gravedad.
La velocidad inicial se compone de dos partes:
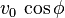 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial. - En lo sucesivo

- En lo sucesivo
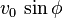 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial. - En lo sucesivo
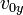
- En lo sucesivo
Se puede expresar la velocidad inicial de este modo:
 : [ecu. 1]
: [ecu. 1]
Será la que se utilice, excepto en los casos en los que deba tenerse en cuenta el ángulo de la velocidad inicial.
Ecuación de la aceleración
La única aceleración que interviene en este movimiento es la de la gravedad, que corresponde a la ecuación:
que es vertical y hacia abajo.
Ecuación de la velocidad
La velocidad de un cuerpo que sigue una trayectoria parabólica se puede obtener integrando la siguiente ecuación:
La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
Esta ecuación determina la velocidad del móvil en función del tiempo, la componente horizontal no varía, mientras que la componente vertical sí depende del tiempo y de la aceleración de la gravedad.
Ecuación de la posición
Partiendo de la ecuación que establece la velocidad del móvil con relación al tiempo y de la definición de velocidad, la posición puede ser encontrada integrando la siguiente ecuación diferencial:
La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
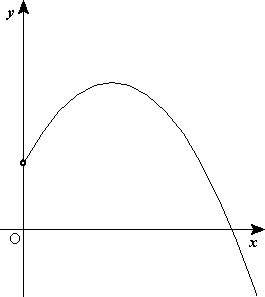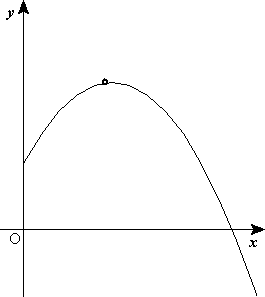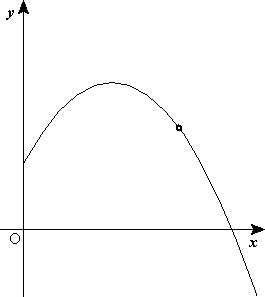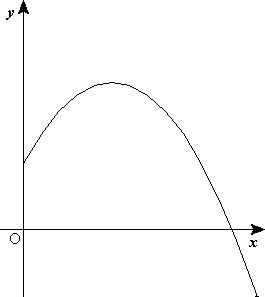
La trayectoria del movimiento parabólico está formada por la combinación de dos movimientos, uno horizontal de velocidad constante, y otro vertical uniformemente acelerado; la conjugación de los dos da como resultado una parábola.
Movimiento parabólico con rozamiento
La presencia en el medio de un fluido, como el aire, ejerce un fuerza de rozamiento que depende del módulo de la velocidad y es de sentido opuesto a esta. En esas condiciones, el movimiento de una partícula en un campo gravitatorio uniforme no sigue estrictamente una parábola y es sólo casi-parabólico. En cuanto a la forma del rozamiento se distinguen dos casos.
Movimiento a baja velocidad
Para un fluido en reposo y un cuerpo moviéndose a muy baja velocidad, el flujo alrededor del cuerpo puede considerarse laminar y, en ese caso, el rozamiento es proporcional a la velocidad. La ecuación de la trayectoria resulta ser:
donde:
 es la altura inicial desde la que cae el cuerpo.
es la altura inicial desde la que cae el cuerpo. son dos parámetros que definen el problema en términos de las magnitudes del problema.
son dos parámetros que definen el problema en términos de las magnitudes del problema. son la masa del cuerpo que cae, la aceleración de la gravedad, el coeficiente de rozamiento y la velocidad horizontal inicial.
son la masa del cuerpo que cae, la aceleración de la gravedad, el coeficiente de rozamiento y la velocidad horizontal inicial.
Para alturas suficientemente grandes el rozamiento del aire hace que el cuerpo caiga según una trayectoria cuyo último tramo es prácticamente vertical, al ser frenada casi completamente la velocidad horizontal inicial.
Movimiento a velocidad moderada o grande
A velocidades moderadamente grandes o grandes, o cuando el fluido está en movimiento, el flujo alrededor del cuerpo es turbulento y se producen remolinos y presiones que generan una fuerza de frenado proporcional al cuadrado de la velocidad.
En lugar de las ecuaciones anteriores, más difíciles de integrar, se puede usar en forma aproximada las siguientes ecuaciones:
Para esas ecuaciones la trayectoria viene dada por:
Donde:
 es la altura inicial desde la que cae el cuerpo.
es la altura inicial desde la que cae el cuerpo. son dos parámetros que definen el problema en términos de las magntiudes del problema.
son dos parámetros que definen el problema en términos de las magntiudes del problema. son la aceleración de la gravedad, el coeficiente de rozamiento y la velocidad horizontal inicial.
son la aceleración de la gravedad, el coeficiente de rozamiento y la velocidad horizontal inicial.
| ||



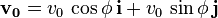



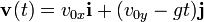
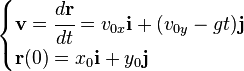


![y(x) = h_0 - \delta \left[\frac{x}{\beta\delta}-\ln \left(1-\frac{x}{\beta\delta} \right) \right]](http://upload.wikimedia.org/math/e/3/1/e31cbaa9061dfc54b45dc4e2a0bd7da8.png)


![y(x) = h_0 - \delta \ln \left[\cosh \left( \frac{e^{x/\delta}-1}{\beta}\right) \right]](http://upload.wikimedia.org/math/5/8/0/580d709c14a395cdf8e2edb1ef710981.png)









0 Response to "El movimiento Bidimencional Parabolico"
Publicar un comentario